Таблица КБМ 2020 — рассчитываем класс бонус-малус
Калькулятор
переплаты
по ОСАГО
Ваш стаж (полных лет)
Если у вас было ДТП
Результат может отличаться в зависимости от наличия ДТП по вашей вине.
Калькулятор
переплаты
по ОСАГО
Текущий класс водителя (КБМ)
Узнать КБМ (бесплатно)
М
2.450
2.31
1.552
1. 4
43
14
0.955
0.96
0.857
0.88
0.759
0.710
0.6511
0.612
0.5513
0.5
Калькулятор
переплаты
по ОСАГО
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Скидка на ОСАГО больше, чем Вам полагается.
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Ваш КБМ соответствует стажу.
В рамках закона цена по ОСАГО определяется по тарифам, которые утверждены на законодательном уровне. При этом важно учитывать, что они одинаковы для всех страховщиков, которые продают защиту лично или онлайн.
Делая расчет, учитывается такой показать, как коэффициент бонус-малус (КБМ). Данный показатель определяется по специальной таблице КБМ 2020, которая с 2002 года остается неизменной.
| Класс | КБМ | Подорожание – Скидка | Количество страховых случаев (выплат), произошедших в период действия предыдущих договоров ОСАГО | ||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||
| Класс, который будет присвоен | |||||||
| M | 2,45 | 145% | 0 | M | M | M | M |
| 0 | 2,3 | 130% | 1 | M | M | M | M |
| 1 | 1,55 | 55% | 2 | M | M | M | M |
| 2 | 1,4 | 40% | 3 | 1 | M | M | M |
| 3 | 1 | нет | 4 | 1 | M | M | M |
| 4 | 0,95 | 5% | 5 | 2 | 1 | M | M |
| 5 | 0,9 | 10% | 6 | 3 | 1 | M | M |
| 6 | 0,85 | 15% | 7 | 4 | 2 | M | M |
| 7 | 0,8 | 20% | 8 | 4 | 2 | M | M |
| 8 | 0,75 | 25% | 9 | 5 | 2 | M | M |
| 9 | 0,7 | 30% | 10 | 5 | 2 | 1 | M |
| 10 | 0,65 | 35% | 11 | 6 | 3 | 1 | M |
| 11 | 0,6 | 40% | 12 | 6 | 3 | 1 | M |
| 12 | 0,55 | 45% | 13 | 6 | 3 | 1 | M |
| 13 | 0,5 | 50% | 13 | 7 | 3 | 1 | M |
Таблица КБМ состоит из нескольких основных разделов:
- класс на начало срока страхования по полису;
- коэффициент, который учитывается в формуле при расчете;
- класс, который учитывается при заключении нового полиса, в зависимости от наличия или отсутствия страховых случаев.

Обратите внимание! Стоит принимать к сведению, что аварийный КБМ на новый срок применяется только в том случае, если застрахованный водитель был виновником ДТП.
Когда собственник машины или участник движения впервые посещает офис страховой, с целью покупки защиты, ему присваивается начальный — 3 класс. Именно от него будет происходить расчет вверх и вниз по таблице.
Пример № 1
После первого года действия ОСАГО у застрахованного водителя не было аварий. При расчете нового договора страховщик использует 4 класс, которому соответствует скидка 5%.
Для определения выполняется несколько простых шагов:
- Смотрится по таблице класс по полису ОСАГО, у которого заканчивается срок действия и необходимо продлить. В данном случае он равен 3 классу.
- После в верхнем разделе таблице определяется количество ДТП по вине застрахованного. Согласно приведенному примеру клиент управлял машиной без аварий.

- По столбику вниз следует опуститься до класса, который действовал на момент страхования и посмотреть новый. В нашем случае – это 4 класс.
- Посмотреть первый столбец таблице, где видно, что 4 классу соответствует коэффициент 0,95. Простыми словами, за год без аварий клиент получил бонус в размере 5%.
Пример № 2
Клиент проездил год и по ранее оформленному бланку у него был 11 класс. За весь срок действия страховки водитель стал виновником аварии три раза. При оформлении автогражданки на новый срок страховщик использует КБМ равный 1,55. Получается, ни о каком бонусе не может быть и речи. Наоборот, предусмотрен повышающий.
Для расчета выполняется несколько простых шагов:
- Смотрится по таблице класс, который был у водителя на момент ранее купленного договора. В нашем случае это 11 класс.
- После по верхней таблице определяется количество случаев. Данный водитель 3 раза был виновником аварии.
- Находясь на столбце с количеством аварий спуститься вниз до строчки с действующим классом и смотрится новый.
 В нашем примере это 1 класс аварийности.
В нашем примере это 1 класс аварийности. - В первом столбце таблицы определяется новый показатель, который равен 1 КБМ. Клиент получает повышающий в размере 1,55. Получается, застрахованный участник движения на 55% переплатит от базовой стоимости договора за свою аварийность.
Калькулятор
переплаты
по ОСАГО
Ваш стаж (полных лет)
Если у вас было ДТП
Результат может отличаться в зависимости от наличия ДТП по вашей вине.
Калькулятор
переплаты
по ОСАГО
Текущий класс водителя (КБМ)
Узнать КБМ (бесплатно)
М
2. 45
450
2.31
1.552
1.43
14
0.955
0.96
0.857
0.88
0.759
0.710
0.65 6″>12
0.5513
0.5
11
0.6Калькулятор
переплаты
по ОСАГО
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Скидка на ОСАГО больше, чем Вам полагается.
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Ваш КБМ соответствует стажу.
КБМ (коэффициент бонус малус) — что это и как влияет на ОСАГО
Калькулятор
переплаты
по ОСАГО
Ваш стаж (полных лет)
Если у вас было ДТП
Результат может отличаться в зависимости от наличия ДТП по вашей вине.
Калькулятор
переплаты
по ОСАГО
Текущий класс водителя (КБМ)
Узнать КБМ (бесплатно)
М
2.450
2.3 55″>2
1.43
14
0.955
0.96
0.857
0.88
0.759
0.710
0.6511
0.612
0. 55
5513
0.5
1
1.55Калькулятор
переплаты
по ОСАГО
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Скидка на ОСАГО больше, чем Вам полагается.
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Ваш КБМ соответствует стажу.
При расчете суммы полиса ОСАГО менеджер или страховой агент учитывает такой показать, как КБМ. Важно знать, что это коэффициент, который напрямую зависит от количества или отсутствия выплат по ДТП водителя и влияет на окончательную стоимость договора.
Важно знать, что это коэффициент, который напрямую зависит от количества или отсутствия выплат по ДТП водителя и влияет на окончательную стоимость договора.
КБМ (коэффициент бонус-малус или скидка за безаварийную езду) — это история водителя, один из коэффициентов, который влияет на стоимость полиса ОСАГО. Может быть повышающим и понижающим в зависимости от наличия ДТП по вине водителя. Если ранее для расчета использовали специальную таблицу КБМ, то сегодня все данные автоматически хранятся на едином портале РСА.
Согласно закону действующие участники рынка должны предоставлять сведения на портал по каждому оформленному полису. Получить отчет по бонусу может каждый желающий совершенно бесплатно.
Важно учитывать, что если полис оформляется при условии «к управлению допущены любые водители» то коэффициент учитывается за собственником и транспортным средством. Даже если во время аварии за рулем будет другой водитель, переплачивать за аварийность придется владельцу машину.
В случае, когда в бланк вписывается несколько водителей, страховщик обязан проверить бонус каждого и при расчете применить минимальный.
Калькулятор
переплаты
по ОСАГО
Ваш стаж (полных лет)
Если у вас было ДТП
Результат может отличаться в зависимости от наличия ДТП по вашей вине.
Калькулятор
переплаты
по ОСАГО
Текущий класс водителя (КБМ)
Узнать КБМ (бесплатно)
М
2.450
2.31
1. 55
552
1.43
14
0.955
0.96
0.857
0.88
0.759
0.710
0.6511
0.612
0.55 5″>
13
0.5Калькулятор
переплаты
по ОСАГО
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Скидка на ОСАГО больше, чем Вам полагается.
Калькулятор
переплаты
по ОСАГО
Поздравляем!
Ваш КБМ соответствует стажу.
Загрузка…Понравилась статья? Поделиться с друзьями:
Правила расчета КБМ в 2020 году
Добрый день, уважаемый читатель.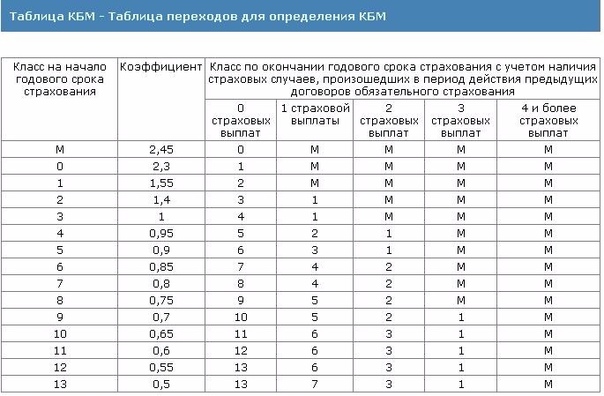
Для начала хочу напомнить, что с 9 января 2019 года вступили в силу новые тарифы ОСАГО, речь о которых шла в отдельной статье. Однако часть указания Центрального банка, относящаяся к расчету КБМ, вступила в силу позже.
Предусмотрены два переходных периода (до 1 апреля 2019 года и до 1 апреля 2020 года). И только начиная с 1 апреля 2020 года новые правила расчета КБМ заработали полностью.
КБМ — это индивидуальный коэффициент водителя, который позволяет получить скидку за безаварийное вождение.
В этой статье речь пойдет о правилах расчета КБМ в разные периоды времени. Кроме того, будет рассмотрено несколько примеров, помогающих лучше понять суть нововведений.
Полис с ограниченным числом водителей
В первой части статьи рассмотрим самый популярный вариант полиса — полис, в котором указан список водителей, допущенных к управлению.
При расчете стоимости такого полиса выбирается максимальное значение КБМ среди всех водителей. В этом вопросе ничего не изменилось.
Например, если Александр имеет КБМ=0.8, а Борис имеет КБМ=0.65, то при расчете стоимости полиса следует использовать коэффициент 0.8.
Таблица изменения КБМ
Таблица, по которой вычисляется значение КБМ на текущий период, также в целом осталась без изменений. Она имеет следующий вид:
| N п / п | Коэффициент КБМ на период КБМ | Коэффициент КБМ | ||||
| 0 страховых возмещений за период КБМ | 1 страховое возмещение за период КБМ | 2 страховых возмещения за период КБМ | 3 страховых возмещения за период КБМ | Более 3 страховых возмещений за период КБМ | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 2,45 | 2,3 | 2,45 | 2,45 | 2,45 | 2,45 |
| 2 | 2,3 | 1,55 | 2,45 | 2,45 | 2,45 | 2,45 |
| 3 | 1,55 | 1,4 | 2,45 | 2,45 | 2,45 | 2,45 |
| 4 | 1,4 | 1 | 1,55 | 2,45 | 2,45 | 2,45 |
| 5 | 1 | 0,95 | 1,55 | 2,45 | 2,45 | 2,45 |
| 6 | 0,95 | 0,9 | 1,4 | 1,55 | 2,45 | 2,45 |
| 7 | 0,9 | 0,85 | 1 | 1,55 | 2,45 | 2,45 |
| 8 | 0,85 | 0,8 | 0,95 | 1,4 | 2,45 | 2,45 |
| 9 | 0,8 | 0,75 | 0,95 | 1,4 | 2,45 | 2,45 |
| 10 | 0,75 | 0,7 | 0,9 | 1,4 | 2,45 | 2,45 |
| 11 | 0,7 | 0,65 | 0,9 | 1,4 | 1,55 | 2,45 |
| 12 | 0,65 | 0,6 | 0,85 | 1 | 1,55 | 2,45 |
| 13 | 0,6 | 0,55 | 0,85 | 1 | 1,55 | 2,45 |
| 14 | 0,55 | 0,5 | 0,85 | 1 | 1,55 | 2,45 |
| 15 | 0,5 | 0,5 | 0,8 | 1 | 1,55 | 2,45 |
Примечание. На самом деле небольшие изменения в таблицу все же будут внесены, однако основную ее часть (коэффициенты) они не затронут.
На самом деле небольшие изменения в таблицу все же будут внесены, однако основную ее часть (коэффициенты) они не затронут.
Примеры при покупке страхового полиса
Рассмотрим несколько ситуаций, в которых могли оказаться водители в январе 2019 года (до введения новых правил):
Владимир. Владимир не владел автомобилем. Последний договор ОСАГО, в который он был вписан, закончился 20 марта 2018 года. КБМ в последнем договоре 0.55.
Галина. Последняя страховка Галины закончилась 10 апреля 2018 года. КБМ в этом договоре 0.65.
Дмитрий имел действующий договор ОСАГО, срок окончания которого — 15 марта 2019 года. Текущее значение КБМ 0.75.
Елена была вписана в страховку ОСАГО, которая закончилась 15 августа 2019 года, значение КБМ 0.85.
Жанна имела в собственности 2 автомобиля. Первый договор ОСАГО заканчивался 15 марта 2019 года, КБМ 0.5. Второй договор заканчивался 15 августа 2019 года, КБМ 0.8 (был один страховой случай).
Зинаида имела действующий договор ОСАГО, который заканчивался 15 августа 2019 года.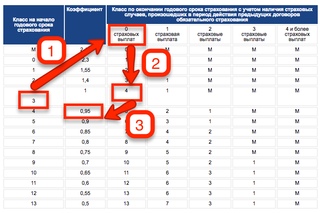 При заключении договора КБМ Зинаиды был равен 0.7, однако 15 января 2019 года по вине Зинаиды произошло ДТП.
При заключении договора КБМ Зинаиды был равен 0.7, однако 15 января 2019 года по вине Зинаиды произошло ДТП.
Такое большое количество ситуаций приведено неслучайно. Просто найдите в списке пример, который лучше всего соответствует Вашей ситуации с КБМ, и далее в тексте статьи ориентируйтесь именно на этот пример.
Если Вы имеете действующий полис и не попадали в ДТП, то наиболее подходящие примеры — Дмитрий и Елена.
Расчет КБМ до 1 апреля 2019 года
До 1 апреля 2019 года при расчете КБМ применялись те же самые правила, что и действовали ранее. То есть коэффициент КБМ пересчитывался по таблице в момент обращения водителя в страховую для покупки следующего полиса.
При этом учитывались только данные действующих страховых полисов, а также полисов, которые прекратили действовать за последний год.
Пример — покупка страховки до 1 апреля 2019 года.
Владимир. При покупке страховки до 20 марта 2019 года данные старого полиса должны быть учтены, т.е. новый КБМ будет равен 0. 5.
5.
Если же Владимир купил страховку после этой даты (25 марта 2019 года), то его КБМ «обнулился» и стал равен 0.5.
Галина. При покупке страховки до 31 марта 2019 года данные старого полиса были учтены, и КБМ стал равен 0.6.
Дмитрий. Если Дмитрий приобрел новый автомобиль и купил на него страховку до 15 марта, то в полисе использовался тот же самый коэффициент, что и в предшествующем, т.к. год еще не прошел. КБМ = 0.75.
Если Дмитрий просто продлил полис 15 марта или позже, то был использован новый коэффициент КБМ = 0.7.
Елена. Поскольку действие предшествующего полиса не закончилось, КБМ в новом полисе остался тем же — 0.85.
Жанна. При продлении договора на первый автомобиль 15 марта 2019 года был учтен совершенный ранее страховой случай, т.е. размер КБМ = 0.8.
Зинаида. В данном случае также имел место один страховой случай, поэтому при покупке ОСАГО КБМ = 0.9
Примечание. Полные правила расчета КБМ, которые действовали до 1 апреля 2019 года, приведены на этой странице.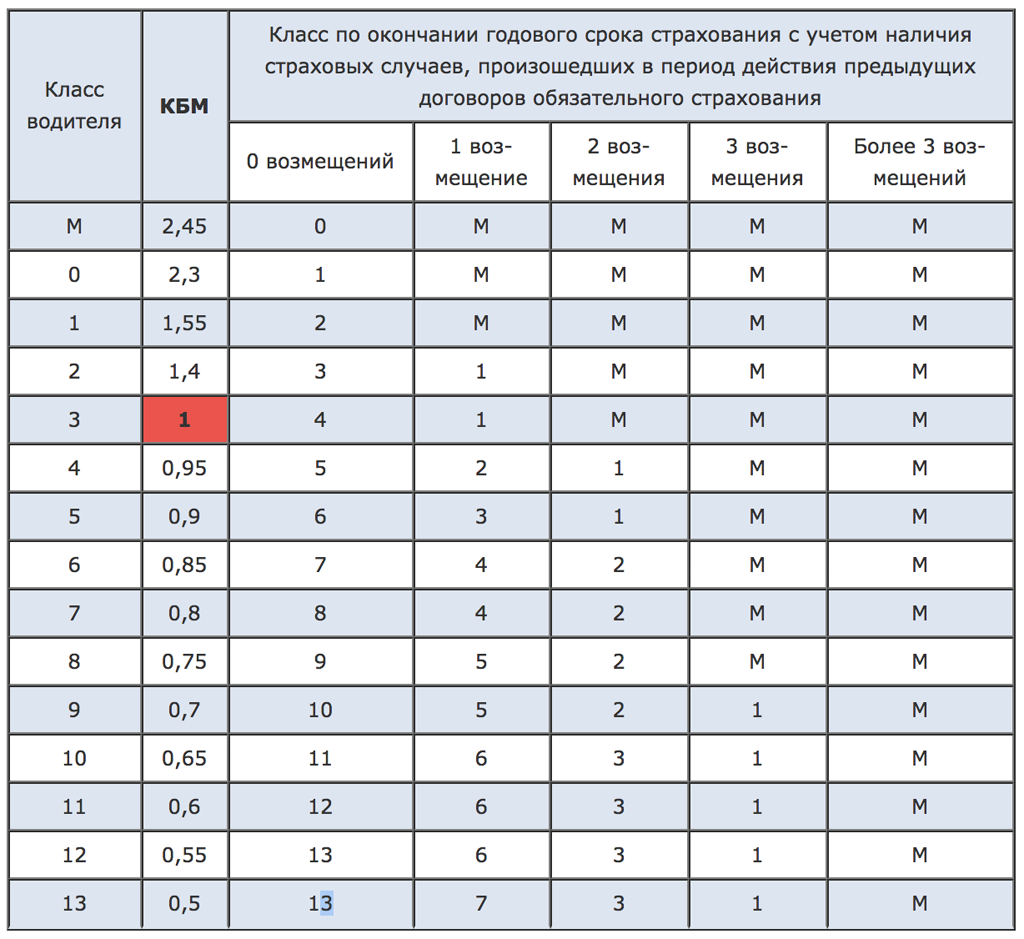
Расчет КБМ с 1 апреля 2019 года по 1 апреля 2020 года
С 1 апреля 2019 года при расчете КБМ действовали следующие правила:
- КБМ рассчитывался 1 апреля 2019 года и действовал в течение года (по 31 марта 2020 года), т.е. один и тот же КБМ применялся при заключении всех договоров ОСАГО.
- В качестве КБМ выбиралось минимальное значение КБМ среди договоров, которые еще действовали 1 апреля 2019 года, а также среди договоров, которые перестали действовать с 1 апреля 2018 года по 31 марта 2019 года.
- КБМ корректировался с учетом количества страховых случаев, которые произошли с 1 апреля 2017 года по 31 марта 2019 года. При этом не учитывались те страховые случаи, которые ранее были учтены при вычислении минимального КБМ.
- Если последний договор ОСАГО водителя закончился до 1 апреля 2018 года, то КБМ = 1.
- Если водитель ранее не был вписан в ОСАГО, то КБМ = 1.
Правила довольно мудреные, поэтому разберем их на примерах:
Пример — пересчет КБМ 1 апреля 2019 года.
Владимир. Последний договор перестал действовать ранее 1 апреля 2018 года, т.е. КБМ = 1 (обнуляется).
Если же Владимир купил страховку до 20 марта 2019 года (см. пример выше) с коэффициентом 0.5, то при пересчете 1 апреля 2019 года за ним сохранился КБМ = 0.5.
Галина. Договор Галины перестал действовать 10 апреля 2018 года, т.е. последний КБМ должен быть учтен при расчете нового значения. Страховых случаев не было. КБМ = 0.6.
Дмитрий имел действующий договор ОСАГО, который к моменту пересчета КБМ закончился. Тем не менее КБМ из этого договора должен учитываться. Кроме того, Дмитрий не был виновником ДТП. КБМ = 0.7.
Если же Дмитрий продлил договор ОСАГО 15 марта 2019 года (см. пример выше) с коэффициентом 0.7, то при пересчете КБМ 1 апреля 2019 года ему присвоен КБМ = 0.65.
Елена. Договор Елены являлся действующим и закончился уже после 1 апреля 2019 года. Однако коэффициент все равно был пересчитан 1 апреля и его размер составил 0.8.
Жанна. При расчете учитывались коэффициенты из двух ранее заключенных договоров (0.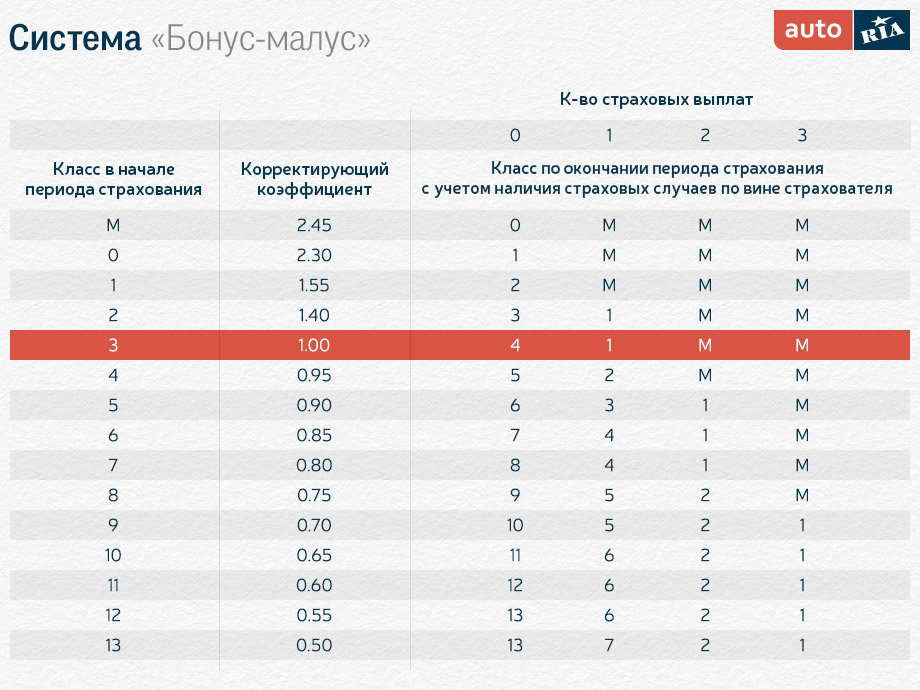 8 и 0.5). Минимальное значение — 0.5. Также был учтен и страховой случай, т.е. КБМ = 0.8.
8 и 0.5). Минимальное значение — 0.5. Также был учтен и страховой случай, т.е. КБМ = 0.8.
Зинаида. Для расчета использовалось предыдущее значение 0.7, а также один страховой случай. КБМ = 0.9.
Примечание. Полные правила расчета КБМ, которые действовали с 1 апреля 2019 года до 1 апреля 2020 года, приведены на этой странице.
Расчет КБМ с 1 апреля 2020 года
С 1 апреля 2020 года при расчете КБМ действуют следующие правила:
- КБМ рассчитывается ежегодно 1 апреля и действует в течение года.
- Для расчета выбирается значение КБМ, рассчитанное на предыдущий период, в котором водитель страховался (с 1 апреля по 31 марта).
- КБМ корректируется с учетом количества страховых случаев, которые произошли за предыдущий период с 1 апреля по 31 марта.
- Если водитель ранее не был вписан в ОСАГО, то КБМ = 1.
Правила становятся проще, однако рассмотрим несколько примеров:
Дмитрий продлил ОСАГО 15 марта 2019 года (КБМ = 0.7), однако 15 ноября 2019 года по его вине произошло ДТП. Тем не менее 15 марта 2020 года Дмитрий продлил ОСАГО с КБМ = 0.65, т.к. страховой случай не оказал влияния на текущий период. Однако в следующем периоде (1 апреля 2020 года) страховой случай был учтен и КБМ стал равен 0.85.
Тем не менее 15 марта 2020 года Дмитрий продлил ОСАГО с КБМ = 0.65, т.к. страховой случай не оказал влияния на текущий период. Однако в следующем периоде (1 апреля 2020 года) страховой случай был учтен и КБМ стал равен 0.85.
Елена продлила страховку 15 августа 2019 года (КБМ = 0.8) и по ее вине произошло ДТП 15 ноября 2019 года. При покупке следующего страхового полиса используется коэффициент, рассчитанный 1 апреля 2020 года и равный 0.95.
Зинаида продлила страховку 15 августа 2019 года (КБМ = 0.9) и не имеет страховых случаев. 1 апреля 2020 года КБМ был пересчитан и принял значение 0.85.
Примечание. Полные правила расчета КБМ с 1 апреля 2020 года приведены на этой странице.
Открытый полис (без ограничения водителей)
Иван имеет в собственности 2 автомобиля:
Корвет. Страховка ограниченная. Единственный водитель — Иван. КБМ = 0.7.
Ленд Крузер. Страховка без ограничений. КБМ владельца = 0.7.
До 1 апреля 2019 года
КБМ рассчитывался только для владельца транспортного средства. Расчет происходил по той же таблице, что и при ограниченном числе водителей. При этом КБМ использовался при расчете открытой страховки.
Расчет происходил по той же таблице, что и при ограниченном числе водителей. При этом КБМ использовался при расчете открытой страховки.
Если страховка Ивана на Ленд Крузер закончилась до 1 апреля 2019 года, то при расчете следующего полиса был использован КБМ = 0.65.
С 1 апреля 2019 года по 1 апреля 2020 года
При расчете стоимости открытого полиса КБМ владельца не учитывался, т.е. он всегда был равен 1.
Однако, сам КБМ для владельца автомобиля все же вычислялся ежегодно (1 апреля) и хранился в базе данных РСА. Он мог использоваться при покупке ограниченной страховки.
1 апреля 2019 года КБМ для Иван пересчитан и принял значение 0.6.
При расчете страховки с ограничениями на Корвет 15 марта 2020 года был использован КБМ = 0.6.
При расчете открытой страховки на Ленд Крузер 15 марта 2020 года использовался КБМ = 1.
То есть, если страховка открытая, то коэффициент за автовладельцем закреплен, однако при расчете стоимости полиса он не используется. Этот факт можно использовать в своих интересах:
Этот факт можно использовать в своих интересах:
Предположим, что водитель допустил несколько ДТП и его КБМ = 2.45. В этом случае он может приобрести открытую страховку (с КБМ = 1), а уже на следующий год его КБМ будет равен 2.3.
Процедуру можно повторять до тех пор, пока покупка с ограничениями вновь не станет выгодной.
С 1 апреля 2020 года
Правила расчета остались теми же самыми:
- При расчете стоимости открытой страховки используется КБМ = 1.
- Реальный КБМ владельца ежегодно пересчитывается и хранится в базе РСА.
1 ноября 2019 года Михаил, находящийся за рулем автомобиля Ленд Крузер (с открытой страховкой), стал виновником ДТП.
1 апреля 2020 года коэффициент для владельца автомобиля Ивана был пересчитан с учетом ДТП. Его новое значение — 0.85.
При расчете страховки с ограничениями на Корвет 15 марта 2021 года будет использоваться КБМ = 0.85.
При расчете открытой страховки на Ленд Крузер 15 марта 2021 года используется КБМ = 1.
Обратите внимание на этот пример. В данном случае виновником ДТП стал Михаил, а стоимость страховки увеличилась только у личного автомобиля Ивана.
Подведем итоги данной статьи:
1. Новые правила для расчета КБМ составлены очень сложно для понимания. Пожалуй, это самый сложный автомобильный нормативный документ, который мне довелось разбирать.
2. В рамках данной статьи подробно разобраны особенности расчета КБМ в различные периоды времени. В целом переход на новую систему не должен создать дополнительных проблем водителям. Многие его просто не заметят.
3. Некоторые читатели pddmaster.ru задают мне вопросы по поводу того, можно ли как-то сэкономить на страховке в переходный период. В данном случае очевидных схем нет. Если и удастся найти какую-то экономию, то она будет минимальной.
4. Серьезные изменения затронули формулу для расчета стоимости открытой страховки. Теперь КБМ автовладельца в формуле не учитывается (равен 1).
В заключение предлагаю Вам изучить подробную статью про коэффициент КБМ:
Удачи на дорогах!
Как узнать класс бонус малус в 2020 году
Коэффициент бонус-малус — это особый расчетный показатель КБМ, который напрямую влияет на стоимость страховки ОСАГО. Подсчет зависит от квалификации самого водителя, который будет пользоваться страховым полисом. В народе КБМ называют скидкой за безаварийное вождение.
Подсчет зависит от квалификации самого водителя, который будет пользоваться страховым полисом. В народе КБМ называют скидкой за безаварийное вождение.
Что такое КБМ
Страховой полис ОСАГО — это обязательный документ любого водителя. Не допускается управление авто без соответствующей страховки. Получают полис через любую страховую компанию, которая имеет соответствующую лицензию и предлагает такие страховые услуги.
На сумму страховки влияет ряд факторов. Это и водительский стаж, и возраст, и марка транспортного средства. Есть даже дополнительная скидка или надбавка за вождение без аварий и нарушений. Например, если водитель в прошлом году ни разу не воспользовался страховкой, то есть не попадал в аварии, то для него стоимость ОСАГО существенно снижается. И наоборот. Если за прошедший год за автолюбителем числились аварийные случаи, то коэффициент увеличит сумму страхования.
Следовательно, коэффициент напрямую влияет на конечную цену ОСАГО. Он определяется в зависимости от наличия страховых случаев в прошедшем страховом периоде.
Как рассчитывается КБМ
Коэффициенты определяются в прямом отношении к количеству страховых случаев. Чем чаще автолюбитель обращается в страховую компанию за выплатами, тем выше его коэффициент аварийности. А следовательно, и выше стоимость страховки. Если водитель продолжительное время не обращался за страховыми премиями, не допускал оплошностей на дороге и не становился участником ДТП, следовательно, ему положена скидка. И чем больше период безаварийности, тем выше бонусы.
По сути, расчет коэффициента бонус-малус по ОСАГО производится на основании присвоенного класса водителя. Затем уже учитывается количество аварий и страховых случаев.
Например, за один год вождения без аварий покупателю ОСАГО причитается скидка в 5%. Дисконт начисляется нарастающим итогом. Максимальное значение скидки — 50%, при которой КБМ равен 0,5. Это нижняя позиция бонус-малус ОСАГО, таблица актуальных значений приведена ниже.
Наличие страховых случаев увеличивает стоимость страховки.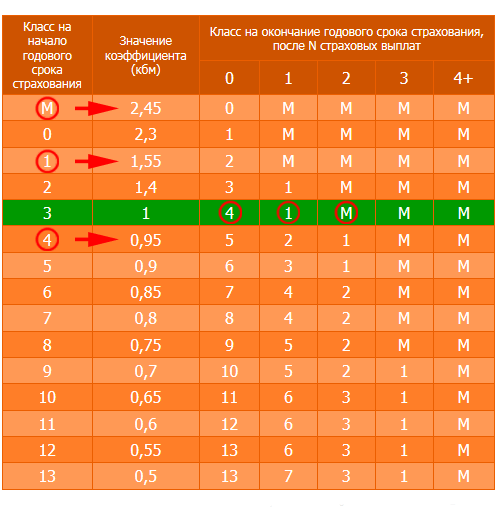 Максимальная сумма накрутки составляет 145%, КБМ равен 2,45.
Максимальная сумма накрутки составляет 145%, КБМ равен 2,45.
Водителю, который заключил договор впервые, присваивается класс 3, для которого КМБ равен 1. Рассчитывать на скидки не стоит. Но и ждать надбавки к цене тоже не придется.
Где проверять
Определить конкретное значение КБМ для водителя можно самостоятельно. Но правильнее проверить КБМ (коэффициент бонус-малус) на официальном сайте Российского союза страховщиков. Сделать это довольно просто. Достаточно лишь заполнить обязательные поля проверочной формы.
Инструкция, как узнать класс бонус-малус:
- Переходим на официальный сайт РСА.
- Указываем дату заключения договора страхования. Здесь вводится или фактическая дата соглашения, или планируемая. Например, если полис приобретаем только в следующем месяце.
- Категорию собственника авто выбираем из предложенных вариантов: компания или простой гражданин. Нужный пункт отмечаем галочкой.
- Выбираем категорию ограничений по количеству лиц, допущенных к вождению на страхуемом авто: неограниченное количество лиц или только конкретный перечень претендентов.

Далее заполняем поля, позволяющие идентифицировать водителя в базе данных. Для этого указываем:
- фамилию, имя и отчество полностью;
- дату рождения в формате ДД.ММ.ГГГГ;
- серию и номер водительского удостоверения — списываем с документа.
Проверяем заполненные поля и нажимаем кнопку поиска. Обратите внимание, что проверка доступна только для граждан РФ. Иностранцы не смогут получить информацию.
Таблица коэффициентов
Актуальные значения для бонус-малус: таблица на 2020 год.
Класс | КБМ | Удорожание или скидка | Количество страховых случаев (выплат), произошедших в период действия предыдущих договоров ОСАГО | ||||
0 | 1 | 2 | 3 | 4 | |||
Присваиваемый класс | |||||||
M | 2,45 | 145% | 0 | M | M | M | M |
0 | 2,3 | 130% | 1 | M | M | M | M |
1 | 1,55 | 55% | 2 | M | M | M | M |
2 | 1,4 | 40% | 3 | 1 | M | M | M |
3 | 1 | нет | 4 | 1 | M | M | M |
4 | 0,95 | 5% | 5 | 2 | 1 | M | M |
5 | 0,9 | 10% | 6 | 3 | 1 | M | M |
6 | 0,85 | 15% | 7 | 4 | 2 | M | M |
7 | 0,8 | 20% | 8 | 4 | 2 | M | M |
8 | 0,75 | 25% | 9 | 5 | 2 | M | M |
9 | 0,7 | 30% | 10 | 5 | 2 | 1 | M |
10 | 0,65 | 35% | 11 | 6 | 3 | 1 | M |
11 | 0,6 | 40% | 12 | 6 | 3 | 1 | M |
12 | 0,55 | 45% | 13 | 6 | 3 | 1 | M |
13 | 0,5 | 50% | 13 | 7 | 3 | 1 | M |
Как пользоваться таблицей для расчета КБМ
Работать с таблицей предельно просто:
- Первая графа — это уровень водителя, который присваивается застрахованному лицу.
 Проверьте класс водителя на сайте РСА. Информацию о классе уточняйте в страховом договоре. Некоторые компании прописывают такие сведения отдельно. А вот остальные источники считаются недостоверными.
Проверьте класс водителя на сайте РСА. Информацию о классе уточняйте в страховом договоре. Некоторые компании прописывают такие сведения отдельно. А вот остальные источники считаются недостоверными. - Вторая графа — это непосредственное значение КБМ. Определяется в зависимости от присвоенного уровня водителя.
- Третья графа определяет размер скидки или надбавки к конечной стоимости полиса. Исходя из этого значения, можно рассчитать бонус-малус и стоимость полиса.
- Четвертая графа — это значение класса, который присваивается при определенном количестве страховых случаев при следующем заключении договоров.
Классы водителя в таблице КБМ
Страховую компанию интересуют только страховые случаи и фактические выплаты премий. То есть если небольшая авария не была зарегистрирована в ГИБДД и гражданин не обращался за страховкой, то такие случаи не влияют на КБМ — коэффициент бонус-малус.
В расчете учитываются только оформленные ДТП, повлекшие за собой страховые выплаты, то есть расходы компании. Каждый случай значительно снижает класс водителя. Например, одна аварийная ситуация отбрасывает автовладельца сразу на несколько позиций. А это приводит к удорожанию полиса.
Каждый случай значительно снижает класс водителя. Например, одна аварийная ситуация отбрасывает автовладельца сразу на несколько позиций. А это приводит к удорожанию полиса.
Пример расчета КБМ
Первоначально водителю присвоен 8 класс, что соответствует КБМ 0,75. То есть ОСАГО он мог приобрести со скидкой в 25%.
Если он допустит одну аварийную ситуацию, то его класс понизится до 5 уровня.
При двух авариях позиции упадут до 2 уровня.
А если страховых случаев больше, то это значит, что клиент является проблемным для страховщика. И ему присвоят минимальный класс М с максимальной суммой надбавки к стоимости полиса.
Если не было аварийных случаев в прошедшем году, то как определить класс бонус-малус? Проверяем по таблице:
Следовательно, водителю при заключении нового договора ОСАГО присвоят уже 9 класс. И он получит скидку в 30%.
Как рассчитывать скидку
За каждый год вождения без страховых случаев автолюбитель может рассчитывать на 5% скидки. Определите конечную стоимость полиса и сумму накрутки или дисконта самостоятельно. Для этого сумму коэффициента вычтите из единицы и переведите полученный результат в проценты.
Определите конечную стоимость полиса и сумму накрутки или дисконта самостоятельно. Для этого сумму коэффициента вычтите из единицы и переведите полученный результат в проценты.
Пример.
Водителю присвоен класс 9. Это КБМ 0,7. Рассчитываем скидку:
(1 — 0,7) × 100% = 30%.
Следовательно, при заключении договора ОСАГО гражданин получить 30% скидку на стоимость страховых услуг.
Считаем Кбм по-новому. Что изменилось в 2020 году?
Новый порядок определения Кбм был описан еще в 2018 году в Указании Банка России № 5000-У, регулирующем процесс расчета цены полиса ОСАГО. Но отдельные пункты данного документа начали действовать лишь в 2020 году.
Реформирование системы определения значения коэффициента бонус-малус разделили на три этапа в привязке к дате начала действия полиса:
- до 31 марта 2019 года;
- с 1 апреля 2019 года по 31 марта 2020 года;
- с 1 апреля 2020 года.
Соответственно, применявшиеся ранее правила более не действуют.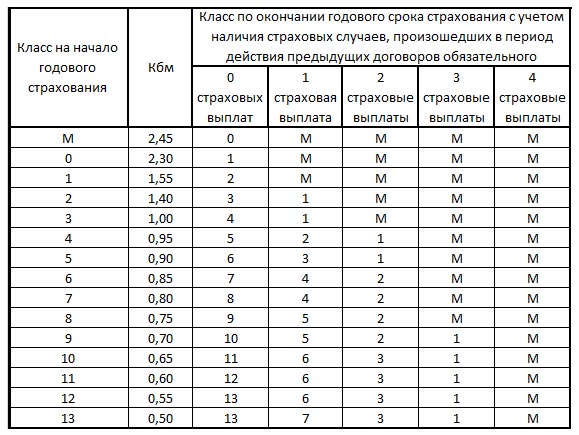 Отныне нужно ориентироваться исключительно на методику определения значения Кбм, действующую с 1 апреля 2020 года.
Отныне нужно ориентироваться исключительно на методику определения значения Кбм, действующую с 1 апреля 2020 года.
Основной посыл изменений в том, что теперь коэффициент бонус-малус более не обнулится при перерыве в страховании более года, а его значение определяется один раз в год и действует для всех полисов ОСАГО , в которые водителя впишут с 1 апреля текущего года по 31 марта следующего за ним года.
Фиксированный Кбм
Таблица значений коэффициента бонус-малус практически не изменилась. Из нее просто убрали классы Кбм, оставив прежние значения скидки в зависимости от количества лет безубыточного страхования. Например, если ранее у водителя не было ни скидки, ни повышающего коэффициента, то после года безубыточного страхования он получит пятипроцентную скидку.
За каждый год страхования без аварий по вине водителя полагается скидка в размере пяти процентов. Максимальная скидка – пятьдесят процентов.
Действующую методику определения Кбм лучше рассмотреть на конкретном примере. Допустим, что предполагается покупка полиса ОСАГО с одним водителем, допущенным к управлению автомобилем. Полис оформляется 10 мая 2020 года.
Допустим, что предполагается покупка полиса ОСАГО с одним водителем, допущенным к управлению автомобилем. Полис оформляется 10 мая 2020 года.
В таком случае при определении значения коэффициента бонус-малус будут использоваться сведения о всех авариях по вине этого водителя за период с 1 апреля 2019 года по 31 марта 2020 года включительно.
Например, если у водителя по предыдущему полису ОСАГО была скидка в размере пяти процентов, и в течение указанного периода он не спровоцировал ни одного ДТП, то скидку увеличат до десяти процентов.
Данная скидка распространяется на все полисы ОСАГО водителя, оформленные в период с 1 апреля 2020 года по 31 марта 2021 года. Если водитель спровоцирует ДТП, скажем, 1 сентября 2020 года, то значение Кбм изменится только по полисам, оформленным после 31 марта 2021 года.
Такая система позволит избежать путаницы при определении Кбм.
Кбм больше не обнулится
Другим важным новшеством стало упразднение возможности обнуления значения коэффициента бонус-малус при перерыве в страховании более года. Ранее возможность обнуления Кбм использовалась как лазейка для «аварийных» водителей.
Например, если в течение года водитель спровоцировал несколько ДТП, и его Кбм существенно увеличивал цену полиса в калькуляторе ОСАГО , то он просто оформлял полис без ограничения по водителям, и через год значение Кбм обнулялось до начального.
Кроме того, такая система была крайне невыгодной для аккуратных и ответственных водителей. При перерыве в страховании более года годами накопленная скидка обнулялась.
Теперь сведения о коэффициенте бонус-малус водителей в базе данных АИС ОСАГО не обнуляются при длительном перерыве в страховании. «Аварийным» водителям придется либо оформлять полис с нулевым Кбм на условии «без ограничений», либо покупать полис с учетом существенного увеличения цены из-за наличия ДТП по их вине.
Как избежать потери Кбм?
К сожалению, ни одна система, даже самая совершенная, не позволяет на сто процентов исключить ошибки. Всегда есть вероятность того, что сотрудник страховой компании допустит опечатку при передаче сведений о полисе ОСАГО в базу данных АИС ОСАГО.
И есть лишь один способ избежать обнуления Кбм вследствие такой ошибки: водителю нужно периодически проверять значение Кбм в базе Российского Союза Автостраховщиков. Для этого достаточно проверить корректность значения бонус-малуса спустя две-три недели после оформления полиса ОСАГО.
Проверить значение Кбм конкретного водителя можно на официальном сайте РСА .
Кроме того, желательно перепроверить значение бонус-малуса после замены водительского удостоверения.
Как известно, клиент обязан уведомить страховую компанию о факте замены этого документа. Чаще всего права меняют из-за истечения срока действия, но в некоторых случаях причиной замены становится смена фамилии.
В обоих случаях есть вероятность ошибки при передаче данных в базу АИС ОСАГО, что приведет к некорректному определению значения Кбм.
Если водитель своевременно узнает о наличии проблем с Кбм после замены прав, то будет значительно проще восстановить скидку. Для этого нужно обратиться с письменным заявлением в компанию, допустившую ошибку при передаче сведений в АИС ОСАГО. Некоторые страховщики разрешают сделать это без личного визита в офис.
расчет класса бонуса малуса водителя
КБМ или коэффициент «Бонус-Малус» — это коэффициент, который используется страховыми компаниями при расчете страховой премии по договору. В зависимости от наличия или отсутствия аварий «Бонус-Малус» может быть понижающим или повышающим. Для удобства определения данного коэффициента создана специальная КБМ таблица по ОСАГО.
| Класс | КБМ | Подорожание – Скидка | Количество страховых случаев (выплат), произошедших в период действия предыдущих договоров ОСАГО | ||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | |||
| Класс, который будет присвоен | |||||||
| M | 2,45 | 145% | 0 | M | M | M | M |
| 0 | 2,3 | 130% | 1 | M | M | M | M |
| 1 | 1,55 | 55% | 2 | M | M | M | M |
| 2 | 1,4 | 40% | 3 | 1 | M | M | M |
| 3 | 1 | нет | 4 | 1 | M | M | M |
| 4 | 0,95 | 5% | 5 | 2 | 1 | M | M |
| 5 | 0,9 | 10% | 6 | 3 | 1 | M | M |
| 6 | 0,85 | 15% | 7 | 4 | 2 | M | M |
| 7 | 0,8 | 20% | 8 | 4 | 2 | M | M |
| 8 | 0,75 | 25% | 9 | 5 | 2 | M | M |
| 9 | 0,7 | 30% | 10 | 5 | 2 | 1 | M |
| 10 | 0,65 | 35% | 11 | 6 | 3 | 1 | M |
| 11 | 0,6 | 40% | 12 | 6 | 3 | 1 | M |
| 12 | 0,55 | 45% | 13 | 6 | 3 | 1 | M |
| 13 | 0,5 | 50% | 13 | 7 | 3 | 1 | M |
Что значат строки в таблице
Стоимость договора напрямую зависит от того, какой будет применен класс КБМ по ОСАГО.
Вся таблица поделена на несколько разделов. В первом столбце указан класс водителя на момент страхования. Водитель, который впервые обращается к представителю компании, с целью оформления полиса, автоматически получает начальный 3 класс. Именно от него будет происходить расчет в большую или меньшую сторону.
Во второй строке указана скидка, коэффициент бонус-малус, в процентном соотношении.
В последнем столбце указано наличие или отсутствие обращений, в течение страхового года.
Как пользоваться таблицей
Пользоваться таблицей очень просто. Для определения коэффициента необходимо знать только: какой класс был на момент страхования и сколько аварийных случаев было в течение действия данного договора. Со вторым значением просто, поскольку каждый водитель знает, случались ли аварии, или нет. Первое значение можно узнать в страховой организации или на странице проверки КБМ.
Для проверки необходимо внести: ФИО, дату рождения, серию и номер водительского удостоверения. После внесения персональных сведений автоматически произойдет проверка.
Для того чтобы лично узнать коэффициент на начало страхования необходимо обратиться в офис компании, где был оформлен договор. При себе необходимо иметь паспорт, оформленный договор и водительское удостоверение. По времени проверка бонус-малус занимает не более 10 минут.
После того как вы узнаете свой класс, необходима таблица КБМ ОСАГО 2018 года, для определения значения. В первом столбце таблице необходимо найти свой класс. Во втором столбце будет отражена скидка, или повышающий коэффициент, который был использован при расчете премии по договору. Далее определяется бонус-малус на следующий год. При отсутствии выплат он опускается вниз по таблице на одну строчку. Если были аварии, он поднимается вверх по таблице, в зависимости от аварий.
Пример расчета КБМ по таблице
Вашему вниманию два примера. В первом случае водитель проездил год без убытков, во втором у водителя были аварии. Рассмотрим, как работает таблица КБМ класса водителя, при отсутствии и наличии страховых случаев.
Иванов Сергей Петрович обратился к страховщику 11 ноября 2015 года. На момент оформления договора водителю присвоили 9 класс КБМ, а именно 30% скидка к базовому тарифу по полису. Получается, клиент уже пользовался услугами страховой компании не один раз и каждый получал 5% за безаварийную езду.
Пример № 1: Отсутствие аварий
Спустя год Сергей Петрович вновь обратился в страховую организацию, для получения нового договора. Как и ранее у клиента не было аварий, и сотрудник предоставила понижающий бонус за безаварийный год. Для определения она использовала таблицу «Бонус-Малус» по ОСАГО.
У Сергея Петровича был 9 класс, двигаясь по этой строке вправо, в таблице, страховой агент посмотрела новый класс, при количестве страховых случаев «0». После 9 идет 10, которому соответствует скидка 0,65 или 35% к итоговой стоимости договора страхования. Получается, по новому договору получит скидку, в размере 35%.
Пример № 2: Наличие трех аварий
Спустя год Сергей Петрович вновь обратился к представителю страховой компании, для оформления нового договора. К сожалению, за последний год у клиента было 3 аварии, по его вине. В связи с этим клиент не рассчитывал на хорошую скидку.
У Сергея Петровича был 9 класс. Двигаясь по строке, нужно посмотреть новый коэффициент, который присваивается водителю, у которого было 3 аварии. Новый класс, который получает аварийный водитель, равен 1 или повышающий коэффициент 1,55. Получается, клиент должен оплатить повышенную страховую премию.
КБМ при неограниченной страховке
Если оформлен полис, по которому предусмотрено неограниченное количество лиц, допущенных к управлению транспортным средством, то возникает вопрос: класс бонуса-малуса, как узнать? В таком случае расчет бонуса идет по собственнику машины.
Коэффициент по собственнику определяется аналогично, как по водителю. Единственное, что стоит принимать во внимание, скидка на машину по собственнику закрепляется на конкретную машину и не распространяется на другие.
К примеру, вы несколько лет подряд, без аварий, оформляете договор на машину ВАЗ 2110 и заработали максимальный класс, в размере 50%. При покупке новой машине, Kia Ria, при условии неограниченного количества лиц, по ОСАГО, вам будет присвоен начальный – 3 показатель. Получается, новая машина – это новая система скидок.
Что такое система Bonus-Malus? (с изображением)
Система «бонус-малус» — это общий термин для широкого спектра систем, которые включают как положительные, так и отрицательные стимулы. Эти системы широко используются в различных деловых контрактах и отношениях, а также в определенных отраслях, например, в страховании. Системы Bonus-Malus позволяют получать конкретные результаты на основе положительного или отрицательного результата.
Предоставляя услуги call-центра клиентскому бизнесу, подрядчик может использовать систему типа «бонус-малус», чтобы удовлетворить позицию клиента в различных результатах.Одним из ярких примеров системы бонус-малус является договорное соглашение между двумя сторонами бизнеса. Например, при предоставлении услуг call-центра или рекламы клиентскому бизнесу, подрядчик может использовать систему типа «бонус-малус», чтобы удовлетворить позицию клиента в различных результатах. Предприятия будут использовать определенные критерии в контракте, чтобы предоставить клиенту либо кредит, либо дебет, в зависимости от того, как услуги работают в течение определенного периода времени.
В мире страхования системы бонус-малус помогают страховщикам и другим сторонам различать держателей полисов на основе их истории требований. Как правило, этот тип системы помогает достичь различных результатов в страховых взносах и других аспектах полисов.С настройкой бонус-малус компания может сделать это в зависимости от того, как страхователь использовал контракт в прошлом. Один из наиболее общих примеров этого — когда страховая компания вносит изменение в платеж или изменение тарифов на услуги, которое основывается либо на количестве прошлых претензий, либо на общей денежной стоимости прошлых претензий.
В некоторых случаях компания может использовать для сотрудников систему бонус-малус.В этих случаях сотрудник получит премию за хорошую работу и уменьшение компенсации за отрицательную работу. Эксперты отмечают, что, хотя бонусные системы распространены во многих сферах бизнеса, включая продажи, система бонус-малус встречается не так часто. Одна из причин этого заключается в том, что у компаний иногда возникают проблемы с набором персонала по модели, включающей отрицательное подкрепление.
Многие утверждали, что различные отрасли и области выиграют от использования системы бонус-малус для повышения производительности труда.Как убедились многие руководители предприятий и правительственные чиновники, эти системы сложно внедрить во многих сферах занятости. Во многом это связано с общим отвращением к использованию негативных стимулов для выполнения работы, что также может привести к снижению морального духа работников в целом. Сопротивление системам «бонус-малус» дает представление о том, как люди обычно относятся к тому, что должно и не должно происходить в рабочем мире.
Соответствие бельгийской системе Bonus-Malus
Калькулятор вероятностей
Глава 95 Введение У большинства статистиков есть набор таблиц вероятности, на которые они ссылаются при выполнении своих статистических работ.Эта процедура предоставляет вам набор электронных статистических таблиц, которые
ПодробнееЧасть 2: Однопараметрические модели
Часть 2: Однопараметрические модели Берноилли / биномиальные модели Вернитесь к iid Y 1, …, Y n Bin (1, θ). Модель выборки / вероятность: p (y 1, …, y n θ) = θ P y i (1 θ) n P y i В сочетании с предыдущим p (θ), байесовский
ПодробнееБонус без претензий? Джон Д.Привет*
Женевские документы о рисках и страховании, 10 (№ 36, июль 1985 г.), 209-228 Бонус за отказ? Джон Д. Эй * 1. Введение Бонусные схемы без претензий являются характерной чертой некоторых договоров страхования, в большинстве случаев
Подробнееα α λ α = = λ λ α ψ = = α α α λ λ ψ α = + β => θ θ β> β β θ θ θ β θ β γ θ β = γ θ> β> γ θ β γ = θ β = θ β = θ β = β θ = β β θ = = = β β θ = + α α α α α = = λ λ λ λ λ λ λ = λ λ α α α α λ ψ + α =
ПодробнееВывод простой линейной регрессии
Вывод простой линейной регрессии 1 Требования к выводу Предположение о нормальности стохастического члена e необходимо для вывода, даже если это не требование OLS.Следовательно, мы имеем: Интерпретация
ПодробнееСвязь между переменными
Содержание 11 Связь между переменными 767 11.1 Введение ……………………… 767 11.1.1 Измерение связи ……. ………. 768 11.1.2 Краткое содержание главы ……………….. 769 11.2 Chi
Подробнее1 Достаточная статистика
1 Достаточная статистика Статистика — это функция T = rx 1, X 2 ,, X n случайной выборки X 1, X 2 ,, X n.Примеры: X n = 1 n s 2 = = X i, 1 n 1 выборочное среднее X i X n 2, выборочная дисперсия T 1 =
ПодробнееГЛАВА 2 Оценка вероятностей
ГЛАВА 2 Оценка вероятностей Машинное обучение Copyright c 2016. Том М. Митчелл. Все права защищены. * ПРОЕКТ от 24 января 2016 г. * * НЕ РАСПРОСТРАНЯЙТЕ БЕЗ РАЗРЕШЕНИЯ АВТОРА * Это
ПодробнееОграниченная оптимизация.
Дополнительные примечания к ams / econ 11b ucsc Оптимизация с ограничениями. c 2010 г., Йонатан Кацнельсон 1. Ограничения Во многих задачах оптимизации, возникающих в экономике, существуют ограничения на значения
. ПодробнееСтатистическое машинное обучение
Статистическое машинное обучение UoC Stats 37700, Зимний квартал Лекция 4: классические линейные и квадратичные дискриминанты.1/25 Линейное разделение Для двух классов в R d: простая идея: разделить классы
Подробнее2. Информационная экономика
2. Информационная экономика В теории общего равновесия все агенты обладали полной информацией относительно любой интересующей переменной (цены, товары, естественное состояние, функция затрат, предпочтения и т. Д.). Подробнее
Департамент математики Индийского технологического института, задание 2-3 в Харагпуре, Вероятность и статистика, март 2015 г.Срок сдачи: 25 марта 2015 г.
Департамент математики Индийского технологического института, задание -3 в Харагпуре, вероятность и статистика, 5 марта. Срок сдачи: 5 марта 2005 г.. Покажите, что функция 0 для x Авторские права c 2005 г., Карл Сигман Среднее значение и дисперсия портфеля Здесь мы изучаем результативность однопериодных инвестиций X 0> 0 (долларов), распределенных между несколькими различными активами.Наш критерий измерения Модели кредитного риска: обзор Пол Эмбрехтс, Рюдигер Фрей, Александр Макнейл ETH Zürich c 2003 (Embrechts, Frey, McNeil) A. Многомерные модели кредитного риска портфеля 1. Моделирование зависимых дефолтов: Психология 7291: Многомерная статистика (Кэри) 27.08.98 Матричная алгебра — 1 Введение в матричную алгебру Определения: Матрица — это набор чисел, упорядоченных по строкам и столбцам.Принято Параметрические модели выживания Херман Родригес [email protected] Весна, 2001 г .; пересмотренная весна 2005 г., лето 2010 г. Мы кратко рассмотрим анализ данных о выживаемости, когда можно принять параметрическое значение Современная актуарная теория риска Современная актуарная теория риска, Амстердамский университет Роба Кааса, Нидерланды Католический университет Марка Гувертса, Левен, Бельгия и Амстердамский университет, Нидерланды 0 ВВЕДЕНИЕ 1 Глава 9 Оценка опыта 0 Введение Рейтинговый процесс — это процесс принятия решения о подходящем уровне страховой премии для определенного класса страхового бизнеса.Содержание Роль бухгалтерского учета в управлении, Ричард А. Янг 1. Введение Одна из важных ролей бухгалтерского учета заключается в оценке актива или фирмы. Когда рынки идеальны, можно оценить активы на их рынке Математика 541: Статистическая теория II Лектор: Сонгфэн Чжэн Оценка максимального правдоподобия 1 Оценка максимального правдоподобия Максимальное правдоподобие — это относительно простой метод построения оценки для ГЛАВА 5 Ошибки округления В двух предыдущих главах мы видели, как числа могут быть представлены в двоичной системе счисления и как это является основой для представления чисел в компьютерах.С любого Экономика страхования В этой последней лекции мы рассмотрим большинство тем экономики информации в одном приложении. Благодаря этому вы увидите, как дифференциальные информационные допущения позволяют У Нила Салкинда (ред.), Энциклопедия исследовательского дизайна. Таузенд-Оукс, Калифорния: Сейдж. 010 Коррекция оранжерей-Гейссера Эрве Абди 1 Обзор и предыстория При проведении дисперсионного анализа с помощью РАСЧЕТЫ И СТАТИСТИКА ВЫЧИСЛЕНИЕ ОЧКОВ Преобразование шкалы от 1 до 5 в баллы от 0 до 100 Когда вы посмотрите свой отчет, вы заметите, что баллы представлены по шкале от 0 до 100, даже если респондентов Бюллетень Том.30, № 33: декабрь 2013 г. Несчастные убытки от возмещения ущерба от пожара Транспортные средства с известными дефектами, связанными с возгоранием, имеют значительно более высокий риск убытков по страхованию от пожаров безаварийного характера по сравнению с автомобилями 1 Модель расширения финансово-сбалансированной системы бонусов-малус Другое: установление оценок, рейтинг опыта XIAO, Центр прикладной статистики Югу, Китайский университет Жэньминь, Пекин, 00872, P.R. China Телефон: адрес: MENG, Центр прикладной статистики Шэнван, Университет Китая Жэньминь, Пекин, 00872, КНР Телефон: адрес: CONGER, Robert the Tillinghast, бизнес Башни Перрин, Чикаго адрес: Резюме: Из-за отсутствия информации раскрытие информации среди страховщиков, страхователь, который платит высокую премию в одной страховой компании, может передать свой полис другой компании, не обязательно имея при себе баллы, связанные с прошлыми претензиями. Когда ставка выбытия страхователя связана со шкалой бонус-малус, т.е.е., держатели полисов с высоким размером страховки с большей вероятностью уйдут из-за высоких страховых взносов, это невозможно для системы бонус-малус (BMS) с конечным числом классов, которая используется для приближения оптимальной BMS с бесконечным количеством классов , чтобы быть финансово сбалансированным. Мы предлагаем BMS, которая предназначена для уменьшения ошибки аппроксимации, когда она используется для приближения к оптимальной BMS, а также для уменьшения финансового дисбаланса. Наш результат напоминает шкалы BMS, используемые на практике, то есть шкалы бонус-малус мягкие: бонусы невысоки, а ошибки также низкие, поэтому финансовый дисбаланс не слишком серьезный.eywords: модель. Бонус-малусная система, квадратичное программирование, цепь Маркова, открытая 2 Модель расширения финансово-сбалансированной системы бонусов-малус XIAO Yugu MENG Центр прикладной статистики Шэнван, Китайский университет Жэньминь, Пекин, 00872, КНР Роберт КОНГЕР, Tillinghast, компания Towers Perrin, Чикаго Краткое содержание: из-за отсутствия информации раскрытие информации среди страховщиков, страхователь, который платит высокую премию в одной страховой компании, может передать свой полис другой компании, не обязательно неся при этом баллы, связанные с прошлыми претензиями.Когда процент ухода держателя полиса соотносится со шкалой бонус-малус, т. Е. Держатели полиса с высоким размером страхового полиса с большей вероятностью уйдут из-за высоких страховых взносов, это невозможно для системы бонус-малус (BMS) с конечным числом классов. который используется для аппроксимации оптимальной BMS, имеющей бесконечное количество классов, чтобы быть финансово сбалансированной. Мы предлагаем BMS, которая предназначена для уменьшения ошибки аппроксимации, когда она используется для приближения к оптимальной BMS, а также для уменьшения финансового дисбаланса.Наш результат напоминает шкалы BMS, используемые на практике, то есть шкалы бонус-малус мягкие: бонусы невысоки, а ошибки также низкие, поэтому финансовый дисбаланс не слишком серьезный. eywords: модель. Бонус-малусная система, квадратичное программирование, цепь Маркова, открытая. Введение Бонус-малусные системы изучались рядом авторов в рамках цепей Маркова. Оптимальные шкалы были выведены Норбергом (976), Борганом, Хоем и Норбергом (98) и Гильдом и Сундтом (989). Сентено и Андраде (2002) вывели оптимальные шкалы для бонусных систем, которые не были марковскими процессами первого порядка.Андраде и Сентено (2005) предложили надбавку, определяемую по геометрической шкале, то есть надбавки между последовательными классами увеличиваются на постоянный процент. Из совершенно другого способа аппроксимации оптимальной BMS с бесконечным числом классов Коэн и Доре (996) дали BMS с конечным числом классов, которая остается в финансовом балансе на протяжении многих лет, путем минимизации квадратичной функции разницы. между BMS и оптимальной BMS. Однако указанные выше методы нельзя использовать непосредственно в открытом портфеле без стационарного распределения, независимого от шкалы премий.Centeno и Andrade (200) изучали системы бонус-малус в открытом портфеле, т. Е. Учитывая, что страхователь может передать свой полис другой страховой компании в любое время. При предположении, что (а) доли рынка заданы экзогенно и (б) вероятность того, что страхователь покинет компанию, не зависит от величины 3 премии страхователя, они доказали, что долгосрочное распределение страхователей по классам BMS не зависит от рыночных долей.Но предположение, что вероятности ухода не зависят от шкалы премий, сомнительно. Фактически, вероятность ухода должна зависеть от шкалы страховых взносов и уровня терпимости страхователя к штрафам за претензии, а также от стоимости передачи его полиса в другую страховую компанию. В частности, в Китае из-за недостаточного раскрытия информации страховщиками может оказаться целесообразным «уклониться» от упущения со стороны одной страховой компании и создать экономию страховых премий, превышающую затраты на получение нового старта в другой компании.Вообще говоря, учитывая уровень толерантности застрахованного к открытому портфелю, шкала страховых взносов влияет на стационарное распределение и затрудняет моделирование системы. Например, если ошибки превышают уровни терпимости застрахованного, то количество уходящих страхователей может быть больше, чем количество новых участников, поэтому количество страхователей среди некоторых классов BMS стремится к нулю. Кроме того, если предположить, что застрахованный покинет компанию с вероятностью 00%, когда ущерб выходит за пределы допустимого уровня страхователя, то штрафы для водителей с историей претензий не могут быть такими высокими, как того требует оптимальная BMS, поскольку нет водители останутся в страховой компании, чтобы оплатить эти штрафы.Чем ниже уровень толерантности страхователя к штрафам, тем труднее создать финансово сбалансированную СЭУ, в результате чего модель, предложенная Коэном и Дореем (996), может не иметь решения. В этой статье мы расширяем модель финансово-сбалансированной BMS, предложенную Коэном и Дореем (996). Мы предлагаем BMS, которая предназначена не только для получения небольшой ошибки приближения к оптимальной BMS, но и для уменьшения финансового дисбаланса. Модель расширения может быть использована для разработки BMS в открытом портфеле и получения решения сложной ситуации, когда застрахованный покинет компанию с вероятностью один, когда malus выходит за пределы допустимого уровня.Это решение ближе к шкалам BMS, которые мы видим на практике, то есть шкалы бонусов и малуса уменьшены до некоторых более мягких уровней, чем было бы указано в оптимальной системе BMS. Оставшаяся часть статьи организована следующим образом. В разделе 2 представлена открытая модель, предложенная Сентено и Андраде (200), и модель финансово сбалансированной BMS, предложенная Коэном и Дореем (996). В разделе 3 представлен случай вероятностей выхода в зависимости от шкалы премий для открытого портфеля. В разделе 4 представлена модель расширения и ее упрощенная версия для открытого портфеля.Раздел 5 дает имитацию и несколько простых примеров с использованием модели расширения. Наконец, в статье представлены некоторые заключительные замечания. 2. Открытая модель и финансово сбалансированная BMS В этом разделе мы представляем открытую модель, предложенную Centeno и Andrade (200), и модель финансово сбалансированной BMS, предложенную Coene и Doray (996). 4 Позвольте представить количество классов системы бонус-малус.Система определяется тремя элементами: шкалой страховых взносов C = (C ,, C), начальным классом k и правилами перехода, которые определяют переход из одного класса в другой, когда количество требований известно. Новый страхователь начнет с класса k. Правила перехода представлены временной матрицей T, элементы которой T (i, j) представляют собой набор чисел требований, которые могут привести страхователя из класса i в любой период в класс j в следующем периоде. Таблица в разделе 5 данной статьи иллюстрирует матрицу T.Каждый страхователь характеризуется параметром риска θ, который считается наблюдаемым значением положительной случайной величины с функцией распределения U (.). Мы будем использовать θ для обозначения страхователя с параметром риска θ., Который, как мы предполагаем, является постоянным во времени. Пусть M n будет количеством требований, поданных страхователем в течение периода [n-, n), n =, 2 ,. Предполагается, что для данного страхователя θ, M n равны i.i.d. случайные переменные. Пусть в течение периода [n -, n]. pθ (m) — вероятность того, что страхователь θ предъявит m требований. Для каждого i = ,, пусть dm, θ (), i 0 dm, θ () i, будет условной вероятностью того, что страхователь θ, находившийся в классе i в период и подал m требований в течение периода, покидает компанию (для удобства представления мы предполагаем, что страхователи покидают компанию только в конце периода).Пусть d (i) θ будет условной вероятностью того, что страхователь покинет компанию в конце периода, когда он в течение периода находился в классе i. Тогда имеем d () i = p (m) d θ () i, θ m = 0 θ m, где p (m) — вероятность того, что страхователь θ подаст m требований в течение одного периода страхования θ. Эту систему можно рассматривать с помощью цепочки Маркова с состояниями +, где состояние, помеченное знаком +, относится к внешнему миру (т. Е. Страхователь покидает компанию). Первые состояния соответствуют классам BMS.Сентено и Андраде (200) назвали эту модель «открытой моделью». И в этой модели вероятности dm, θ () i не обязательно зависят от шкалы премий C = (C ,, C). В закрытом портфеле обычно предполагается, что является гамма-распределенным с параметрами α и β, а pθ (m) — распределенным по Пуассону. Тогда распределение количества требований за один год имеет отрицательное биномиальное распределение, см. Lemaire (995). В этих предположениях Лемер (995) показал, что для оптимального 5 BMS, (т.е., премия страхователя сопоставима с ожидаемой частотой его требований), премия для водителя, подавшего N требований в течение t лет, определяется как C (Nt,) β α + N = α β + t, где мы предполагаем, что страховая премия для нового страхователя (N = 0, t = 0) составляет. Очевидно, что оптимальная BMS имеет бесконечное количество классов (хотя многие из них будут очень малонаселенными). Легко показать, что эта оптимальная BMS является финансово сбалансированной, то есть средняя премия, получаемая страховщиком каждый год, равна средним требованиям.Coene и Doray (996) предложили финансово сбалансированную BMS с конечным числом классов. Их метод заключается в минимизации квадратичной функции разницы между премией оптимальной BMS и премией BMS с конечным числом классов, взвешенной по стационарной вероятности нахождения в определенном классе. Это эквивалентно решению следующей задачи квадратичного программирования min l = (N,) tf CC ll (N, t) 2 () с ограничениями Cl + Cl 0, l =, …, Ck = fc lll = где fl — стационарная вероятность попадания в класс l.Ограничение C l C + l 0, l =, …, гарантирует, что страховая премия увеличивается (или, по крайней мере, не уменьшается) по мере перехода к более высоким (более malus) классам BMS. Ограничение неравенства l = fc ll равно налагается, чтобы обеспечить финансовую сбалансированность портфеля в долгосрочной перспективе, т. е. чтобы средняя собранная премия была по крайней мере равна среднему количеству требований (здесь мы не учитываем расходы). В эту модель могут быть добавлены дополнительные ограничения на надбавки, на что указали Коэн и Доре (996), например, максимум, назначаемый водителю, и максимальный штраф, который плохой водитель может быть ограничен ограничениями C A и C B. 6 3. Случай вероятности ухода в зависимости от шкалы премий для открытого портфеля Мы предполагаем, что новые политики портфеля входят в систему в том же классе k, и страхователь покидает компанию в конце периода, если его премия на предстоящий период выше, чем его уровень терпимости, обозначенный буквой G, независимо от того, к какому классу он принадлежал и сколько требований он подал в истекающий период.Это означает, что у всех страхователей одинаковая манера «уклонения». Это предположение является упрощенным, но мы покажем некоторые эвристические результаты, когда вероятность ухода страхователя зависит только от шкалы премий для открытого портфеля. Согласно сделанному выше предположению, если количество заявок m T (i, j), то dm, θ, если Cj> G () i = 0, если Cj G (2) Таким образом, вероятность ухода dm, θ () i является функция шкалы премий C и уровня допуска G. Поскольку стационарные вероятности цепи Маркова определяются ее матрицей переходных вероятностей, то fl, которая представляет собой стационарную вероятность нахождения в определенном классе l, также является функцией C и Г.Следовательно, модель () может быть изменена на min f (C, G) CC l = (N,) tll (N, t) 2 (3) Cl + Cl 0, l =, …, Ck = fl (C, G) Cl l = Мы видим, что эту модель сложнее решить. Во-первых, долгосрочное распределение не имеет явной формы. Во-вторых, ограничение финансового баланса может не соблюдаться в некоторых типичных случаях, которые будут освещены в разделе Модель расширения для открытого портфеля с уклонением страхователя. Мы предлагаем модель расширения на основе модели (), то есть 7 2 (n) 2 (n) min f (C, G) (,) (,) l Cl CN t + M fl CG Cl l = (N,) tl = (4) C l C l 0, l = + ,…, Ck = (5) Первая часть модели (4) представляет разницу между предлагаемыми шкалами BMS и оптимальными шкалами BMS, поэтому она измеряет ошибку аппроксимации, когда предлагаемые шкалы BMS используются для замены оптимальной BMS. Вторая часть модели (4) представляет финансовую несбалансированность предлагаемой BMS. Таким образом, цель модели (4) — минимизировать ошибку аппроксимации и финансовый дисбаланс одновременно. M — финансово-балансирующий вес в модели (4). Регулируя значение M от нуля до бесконечности, мы можем по-разному акцентировать внимание на финансовом балансе.Чем больше значение M, тем более сбалансированной в финансовом отношении будет предлагаемая BMS. Когда M =, ошибка аппроксимации BMS и финансовый дисбаланс будут взвешены эквивалентно: f (n) — это доля полисов, относящихся к классу l в течение периода n. Здесь мы используем распределение за период n вместо стационарного распределения, которое может не существовать. В той степени, в которой распределение изменяется во времени, C l, полученный из модели (4), также может изменяться во времени. Характеристика финансовой сбалансированности означает, что штрафы для плохих водителей должны быть достаточно жесткими.То есть бонусы, присуждаемые хорошим водителям, должны компенсироваться ошибками от плохих водителей. Как упоминалось выше, оптимальная BMS является справедливой и финансово сбалансированной, но на некоторых рынках она слишком сложна для применения на практике плохих драйверов. Модель расширения дает возможность одновременно учитывать справедливость и финансовый баланс практической BMS для открытого портфеля. В экспериментах, которые мы провели с этой моделью, мы выбрали M как конструктивную характеристику, вместо того, чтобы решать, как M удовлетворять некоторым указанным критериям, но этот альтернативный подход к решению уравнения также может быть исследован дополнительно.Хотя характеристика финансовой сбалансированности очень важна для BMS, почти все BMS на практике не имеют этой характеристики. На практике исправление финансового дисбаланса BMS часто достигается неявно путем загрузки дополнительных резервов в другие элементы рейтинговой схемы; мы полагаем, что предпочтительнее рассматривать влияние финансового дисбаланса непосредственно в рамках проекта BMS. И если уровень терпимости держателя полиса низкий в открытом портфеле, существует ситуация, обсуждаемая в разделе 5, которая делает модель, предложенную Коэном и Дореем (996), не имеет решения.Однако в этой ситуации можно использовать модель (4). Задача оптимизации (4) представляет собой неразрывное нелинейное программирование. Чтобы получить какое-то полезное решение, мы добавляем два предположения. Во-первых, мы предполагаем, что количество новых страхователей, входящих в систему, равно 0. Во-вторых, все шкалы страховых взносов меньше допустимого уровня страхователей. Таким образом, количество уходящих страхователей также равно 0, и система упрощена до закрытой с 8 с учетом G.При этих предположениях стационарная вероятность существует. Следовательно, мы можем получить упрощенную модель для открытого портфеля, то есть min 2 2 fl Cl C (N, t) + M fc ll (6) l = (N,) tl = C l C l 0, l = ,. .., + Ck = CG (7) 5. Моделирование и несколько простых примеров с использованием модели расширения В этом разделе мы даем имитацию, чтобы показать, что финансовый баланс невозможен, требуя, чтобы разница премий между двумя соседними классами была на уровне минимум, скажем 5%. И мы получаем несколько числовых иллюстраций модели расширения для сравнения с примерами из Коэна и Дорея (996).5 .. Случай финансового дисбаланса. Мы рассматриваем BMS, определенную Тейлором (997). Всего 9 классов. 6 класс — стартовый. Если страхователь не подавал никаких претензий в течение периода t, он перемещает на один класс вниз в период t +. Если в течение периода t было заявлено несколько требований, m t> 0, то страхователь перемещает 2m t класса вверх. Правила перехода описаны в Табл. Правила перехода таблицы для BMS — / + 2 Количество претензий, заявленных в период t Уровень класса в период t Результирующий уровень класса в период t Мы предполагаем, что функция распределения параметра риска Θ представляет собой трехточечное дискретное распределение, то есть Pr (θ =) =, Pr (θ =) =, Pr (θ =) =, как было предложено Уолхином (999).Ограничение, что C l + C l> (% от C k)> 0, l = ,, 8, добавляется для получения практической BMS, 9 то есть разумная степень разницы в ценах между классами, что является обычным явлением на практике. Здесь мы устанавливаем a = 5%. Мы не включали сюда финансовое балансирование модели расширения. Для данного значения уровня допуска G существует четыре случая для открытого портфеля.Случай: C 9 G, то есть все страхователи остаются в системе. Случай 2: C 9> GC 8, т. Е. Страхователь покидает компанию, когда он переводится в класс 9. Случай 3: C 8> GC 7, т.е. страхователь покидает компанию, когда он переводится в классы 8 или 9. Случай 4: C 7> GC 6, т. Е. Страхователь покидает компанию, когда страховая премия превышает первоначальную премию. Здесь мы полагаем G = 0,5. Для простоты мы перечисляем только первые три случая в таблице 2. В каждом случае мы используем допущение, что в открытой системе 00% страхователей, для которых установлен размер премии, превышающей G, покинут страховщик, и, таким образом, G будет жесткая верхняя оценка премии C l для любого класса, как в формуле (2).Мы начнем с гипотетического портфеля из 50 000 держателей полисов, первоначально относящегося к классу 6, а количество новых держателей полисов, входящих в систему каждый год, равно 50 000 руб., Где r — постоянная пропорция. N (t) — общее количество страхователей в году t. Таблица 2 содержит моделированное распределение водителей в каждом классе через 40 и 00 лет. Верхняя граница среднего страхового взноса, обозначаемая UBAP, получается путем признания того, что страховой взнос в любом классе не превышает G f (C, G) C (j) (j) f (C, G) + f (C, G) G = UBAP jjjj = j = j = 7 Таблица 2 Распределение драйверов в момент времени t для BMS — / + 2 и UBAP Случай Случай 2 Случай 3 Класс r = 0 r = 0 r = 0.г = 0 г = 0 г = 0. г = 0 г = 0 г = 0. t = 4 t = 0 t = 0 t = 4 t = 0 t = 0 t = 4 t = 0 t = UBAP N (t) Из таблицы 2 мы можем видеть, что верхние границы среднего страхового взноса всегда ниже, чем , что означает неудовлетворение финансового баланса для BMS. Интуитивно страховщик может увеличить количество ошибок для плохих водителей или уменьшить 10 бонусов для хороших водителей с целью увеличения средней премии.Но первый способ не обязательно эффективен для открытого портфеля, когда поведение при уходе похоже на предположение, определенное формулой (2). Если уровень допуска G особенно низок, жесткие весы BMS могут вытеснить из компании как хороших, так и плохих водителей. Более тщательное изучение совокупности держателей полисов через несколько лет в предполагаемых ситуациях, когда поток новых держателей полисов меньше, чем исход (т. Е. R = 0 или мал), покажет, что на самом деле финансовый дисбаланс не совсем такой, как плохо, как показано в таблице 2, потому что доля плохих водителей, которые перешли в более высокий класс и, следовательно, покинули компанию в ответ на C l> G, больше, чем доля хороших водителей, которые покинули компанию (в частности, хорошие водители у которых оказалось достаточное количество требований, чтобы в краткосрочной перспективе превысить размер премии G).Таким образом, требуемая средняя премия может со временем опуститься ниже нуля в этой ситуации. В ситуациях, когда количество новых держателей полисов больше или равно количеству уходящих держателей полисов, нам нужно будет сделать дополнительные предположения о том, какая часть нового бизнеса для нашей компании является действительно свежими драйверами по сравнению с сочетанием факторов, покидающих компании-конкуренты. из-за нетерпимости к страховым взносам и, следовательно, смещения в сторону сочетания плохих факторов, аналогичных сочетанию действующих страхователей.Полное моделирование этого эффекта было бы полезным расширением текущей модели и могло бы включать некоторые интересные соображения по альтернативным предположениям о ценовом поведении конкурентов. В этой статье мы сделали упрощающее предположение, что наша целевая средняя премия остается на уровне 0, что было бы в случае, если бы сочетание хороших и плохих факторов в портфеле не претерпело значительных изменений со временем. В связи с этой же динамикой, если новые держатели полисов склоняются к смеси, сосредоточенной с плохими драйверами, было бы целесообразно рассмотреть возможность установления входного класса для нового бизнеса в классе выше, чем C k =.0, со степенью сдвига, зависящей от предположений или результатов модели в отношении конкретного состава входящих страхователей. С практической точки зрения, поскольку C k + значительно больше 0 во многих BMS, может быть лучше оставить k в качестве начального класса, но установить C k несколько выше 0, возможно, даже в оптимальной BMS, против которой применяется практическая BMS. измеряется, отражая сочетание старых и новых, плохих и хороших драйверов, которые, как ожидается, будут находиться в классе k. Это области для дальнейшего изучения. Некоторые упрощенные примеры с использованием модели расширений. В этом разделе мы получаем числовые иллюстрации модели расширения, описанной в формулах (6) и (7), по сравнению с некоторыми примерами из Coene and Doray (996).Коэн и Доре (996) рассмотрели два BMS. BMS — это система с 8 классами, и новый драйвер начинается с класса 0. Водитель, не получивший претензий в течение года, понижается на один класс, в то время как водитель повышается на два класса для первой претензии в году и три класса для каждого последующего. претензии в том году. BMS2 — это система с 24 классами, и новый драйвер начинается с класса 0. Водитель, не получивший претензий в течение года, понижается на один класс, в то время как водитель поднимается на 3 класса для первого требования в году и 4 класса для каждого последующего. претензии в том году.Коэн и Дорей смоделировали 11 нескольких лет с использованием отрицательного биномиального распределения с параметрами (α =, β =). Для этого анализа они ограничились периодом t = 9 лет и оценили стационарные вероятности и оптимальные шкалы премий нахождения в классе l, обозначенные как fl и C l в наших таблицах 3 и 4. Здесь мы рассматриваем формулу : 2 2 мин fl Cl C (N, t) + M fc lll = (N,) tl = Cl + Cl 0 Cl + Cl a%, l = ,…, 9 C0 = CG (8) Шкалы премий BMS для открытого портфеля показаны в таблице 3 с a = 0 и различными уровнями допуска G и финансово-балансирующими весами M. Средняя премия (AP) увеличивается с увеличением уровень допуска G и коэффициент финансового баланса M. Естественно, что, когда G бесконечно, а M достаточно велико, скажем, M = 00 в таблице 3, шкалы BMS приближаются к шкалам, предложенным Coene и Doray (996), что является отображается в столбце 3 таблицы 3. Также в таблицах 3 и 4 показаны средние премии (AP), полученные в каждом сценарии.В таблице 4, когда коэффициент штрафа G выбран равным 2, шкалы премий от 5 до 24 равны. Это означает, что количество классов должно быть уменьшено до 5. Интересно отметить, что, когда G = 2, M =, a = 5, каждый год без претензий дает экономию 5%, как и старая бельгийская BMS. , хотя правила перехода несколько иные. Более того, когда M достаточно велико и G =, шкала BMS из модели расширения приближается к финансово сбалансированной BMS, разработанной Коэном и Дореем (996), которая отображается в третьем столбце таблицы 4.Кроме того, во всех случаях предполагается, что штраф по первой претензии должен быть более суровым, чем в случае старой бельгийской BMS. Таблица 3 Масштабы премий BMS для открытого портфеля f l Сбалансированная BMS G = M = 00 a = 0 G = M = a = 0 G = 2 M = a = 0 G = 3 M = a = 12 AP Таблица 4 Премиум-шкалы BMS2 для открытого портфеля fl Сбалансированная BMS G = M = 00 a = 0 G = M = 00 a = 5 G = M = a = 0 G = 2 M = a = 0 G = 2 M = a = 5 бельгийских BMS AP 13 6.Заключение Из-за недостаточного раскрытия информации страховщиками на китайском рынке стоимость «уклонения» от неприятностей и получения нового старта в другой компании ниже. Это означает, что штрафы не могут быть достаточно жесткими для плохих водителей, поскольку жесткая BMS может вытеснить как хороших, так и плохих водителей из компании. Мы рассмотрели частный случай, когда вероятности выхода зависят от шкалы премий для открытого портфеля. Мы предложили модель для расчета шкал BMS, и эта модель предназначена для уменьшения ошибки приближения к оптимальным шкалам BMS, а также для уменьшения финансового дисбаланса.Результат модели ближе к шкалам BMS, которые мы видим на практике, то есть шкалы бонусов и малуса уменьшены до некоторых более мягких уровней, чем было бы указано в оптимальной системе BMS. Модель может быть применена к подмножествам застрахованного населения (например, другая шкала BMS для неопытных водителей, чем для опытных водителей), которая будет параллельна некоторой эволюции схем рейтингов страхования на зрелых рынках. Модель продления может быть также применена к ситуации, когда самый высокий страховой взнос регулируется государством (а не поведением страхователя) и должен быть не более G раз больше среднего страхового взноса.В этом случае модель, предложенная Коэном и Дореем (996), может не иметь решения. Одним из недостатков модели продления является предположение, что застрахованный покинет компанию с вероятностью 1, когда malus выходит за пределы его допустимого уровня. Фактически, лучший способ описать поведение уклонения страхователя — это распределение вероятностей. Очевидно, это заслуживает дальнейшего обсуждения. В частности, было бы полезно включить функцию ответа страхователя, которая отражает не только абсолютный уровень премии, но и относительный уровень премии по сравнению с оптимальной премией, чтобы модель могла исследовать последствия неблагоприятного выбора, если цены на хорошие драйверы несколько завышены, а на плохих — несколько занижены, поскольку мы считаем, что это будет довольно распространенным явлением, когда бонусы и недостатки смягчены, и что почти наверняка будет иметь место для многих худших водителей, если максимальная премия будет строго ограничена.Ежегодные изменения цен также могут быть объяснительной переменной уклонения страхователей. Еще более сложное расширение модели будет учитывать поведение конкурентов, поскольку держатели полисов фактически могут реагировать на наличие альтернативных цен на рынке, а не обязательно иметь возможность реагировать на основе (или даже знать) теоретически правильных цен. Мы уверены, что во всех этих дальнейших исследованиях подход с использованием имитационной модели будет более управляемым, чем решение в закрытой форме.Некоторые очень интересные исследования рынка могут помочь осветить и количественно оценить ключевые переменные и параметры ценовой эластичности страхователей. Ссылки [] Андраде и Силва, Дж. М., Сентено, М. Л. (2005). Примечание о бонусных шкалах, Journal of Risk and Insurance, Vol. 72, No. 4, pp 14 [2] Борган, О., Хоэм, Дж. М. и Норберг, Р. (98). Неасимптотический критерий оценки автомобильных бонусных систем, Scandinavian Actuarial Journal, [3] Centeno, M.Л. и Андраде и Сильва, Дж. М. (200). Бонусные системы в открытом портфеле. Страхование: математика и экономика 28 (3), [4] Сентено, М. Л. и Андраде и Сильва, Дж. М. (2002). Оптимальные шкалы бонусов в соответствии с правилами бонусов, зависящих от пути, Scandinavian Actuarial Journal 2, [5] Coene, G. и Doray, L.G. (996). Финансово сбалансированная система бонус-малус, Бюллетень ASTIN, [6] Gilde, V. и Sundt B. (989). О бонусных системах со шкалой достоверности, Scandinavian Actuarial Journal, [7] Lemaire, J. (995). Бонус-малус системы в автомобильном страховании.luwer Academic Publishers, Бостон: Дордрехт: Лондон. [8] Норберг Р. (976). Теория надежности автомобильных бонусных систем. Scandinavian Actuarial Journal 2, [9] Walhin, J. F. и Paris, J. (999), Использование смешанных процессов Пуассона в связи с системами бонус-малус, Бюллетень ASTIN, Этот сайт использует файлы cookie, а также другие части и электронную почту для сбора статистической информации, чтобы узнать, какие рекламные сообщения доступны в прямой линии. Per negare il consnso, clicca qui.
Se prosegui la navigazione accept ad altre are del sito or interagendo con elements del sito manifest il tuo consnso all’uso dei cookies e delle altre tecnologie usate dal sito. Это место с использованием печенья, anche di terze parti, для лучшего опыта навигации. Il Meccanismo Bonus Malus è quello che regola la maggior parte delle polizze assicurative di responsabilità civile delle Automobili в Италии. Il Bonus Malus fa sì che il costo del premio assicurativo di una polizza auto sia semper diverso di anno in anno. Si può pagare di meno, se si è virtuosi e non si provocano incidenti, o pagare di più, se invece si provocano incidenti. Эта система премиум-класса является классическим дивизионом, который соответствует качеству и важен для диверсификации, которая является премией.Le classi vanno generalmente dalla 18, che è la pi alta e costosa, alla 1, la pi bassa ed Economica, con un dislivello che dall’una all’altra triplica il costo del premio. Gli avanzamenti verso l’alto (classe alta, con premio più caro) sono più rapidi di quelli verso il basso (classe bassa, premio meno caro). Это провокация, не имеющая отношения к двум классам на другой стороне бассо. Quando trascorre un intero anno senza incidenti si guadagna una classe verso l’alto. Quindi il sistema del Bonus Malus создан для особого стимула, не противостоящего ничему, как руководству, так и разумному.È статистика, полученная при помощи механического бонуса, имеет некоторые положительные эффекты, связанные с данными, установленными в каждой национальной стране, и ставшей вступительным словом. В реальном времени, этот бонус не является постоянным, но только в том, что касается рекламы или ретроспективного обучения, в одиночку из периода chiamato «di osservazione», который состоит из 2 месяцев, прежде всего, из школы пользы. Si entra nel meccanismo Bonus Malus nella classe 14esima, alla quale corrisponde la cosiddetta price base.Con il passare degli anni poi ci si muove verso l’alto o verso il basso, a seconda che si causino o meno sinistri in seguito ai quali si verifichino danni a cose opersone. Se un sinistro viene provocato dopo la fine di tall periodo verrà incluso nel periodo di osservazione dell’anno successivo e nel бонус malus di 2 anni dopo. Классические качества различных компаний, не имеющих необходимой идентичности, это компании, занимающиеся сбором информации и определенные маржинальные операции, которые управляют и определяют внутренние классы.Для облегчения прохода всех альтракомпаний, и для того, чтобы не далеко выполнять все классические особенности класса заслуг, это статус иституто у системы классического преобразования универсального. Si usano tabelle predisposte dall’IVASS (ex ISVAP) per confrontare la class di merito con la propria compagnia assicurativa (classe interna o contrattuale) Con quella Universale dell’IVASS, che può essere poi tradotta nella classe di merito di qualsiasi assicurativa . Поддержка Поддержка Расчет себестоимости продукции — это определение затрат в денежном выражении на единицу товаров, работ или услуг.В расчет включены прямые и косвенные затраты. Прямые — это стоимость материалов, заработная плата рабочих и т. Д. Косвенные затраты: плановая прибыль, транспортировка и т. Д. Расчётные статьи подробно рассматривать не будем. Автоматизируем процесс расчета плановой себестоимости продукции по формулам Excel. Наша задача — создать таблицу средствами Excel, чтобы при подстановке данных автоматически учитывалась себестоимость товаров, работ, услуг. Себестоимость продукции лучше узнать из сферы торговли.Меньше затрат. Фактически — закупочная цена, выставленная поставщиком; транспортные расходы по доставке товара на склад; пошлины и таможенные сборы, если мы ввозим товары из-за границы. Берем определенную группу товаров. Рассчитываем себестоимость продукции по каждому из них. Последний столбец — коэффициент планируемых производственных затрат — покажет уровень затрат, которые компания понесет на доставку продукции. Заполняем таблицу: Уровень затрат на доставку товаров 1 и 4 составит 10%, 2 и 3 — 15%. Каждая компания рассчитывает плановую себестоимость продукции по-своему. Ведь предприятия несут разные расходы в зависимости от вида деятельности. Любой расчет должен содержать расшифровку затрат на материалы и заработную плату. Расчет плановой себестоимости продукции начинается с определения себестоимости сырья и материалов, используемых для производства товаров (которые непосредственно участвуют в технологическом процессе).Затраты на сырье включены в затраты утвержденных предприятием нормативов за вычетом технологических потерь. Эти данные можно взять в технологическом или производственном отделе. Нормы расхода сырья отразим в таблице Excel: Здесь удалось автоматизировать только один столбец — столбец с расходом с учетом технологических потерь. Формула: = E3 + E3 * F3. Примечание! Для столбца «Технологические потери,%» выставляем процентный формат.Только в этом случае программа рассчитает правильно. Нумерация строк начинается над заголовком. Если данные испорчены, их можно восстановить по номерам. Зная нормы, можем рассчитать стоимость материалов (расчет на тысячи шт.): В этой таблице необходимо вручную заполнить только один столбец — «Цена». Все остальные столбцы относятся к данным листа «Стандарты». В столбце «Сумма» работает формула: = D3 * E3. Следующая статья прямых затрат — это заработная плата производственных рабочих.Учитываются базовая заработная плата и доплата. Принципы начисления заработной платы (сдельная, повременная, от выходной), вы можете узнать в бухгалтерии. В нашем примере расчет заработной платы ведется по нормам выработки: сколько работник определенной квалификации должен заработать за единицу рабочего времени. Данные для расчетов следующие: Цена рассчитывается по формуле: = C3 * D3. Теперь можем посчитать базовую зарплату рабочих: Чтобы заполнить первые два столбца, не считая номера по порядку, мы связали данные этой таблицы с данными предыдущей.Формула расчета бонуса = C3 * 30%. Базовая зарплата = C3 + D3. Дополнительная заработная плата — это все выплаты, производимые по закону, но не связанные с производственным процессом (отпуска, вознаграждение за выслугу лет и т. Д.). Остальные данные для расчета себестоимости продукции мы добавили в таблицу сразу: В столбце «Расчет индикатора» указано место, откуда мы берем данные. 1 Среднее значение и дисперсия портфеля
Модели кредитного риска: обзор
Введение в матричную алгебру
Параметрические модели выживания
Современная актуарная теория риска
Глава 9 Оценка опыта
Управленческая роль бухгалтерского учета
Оценка максимального правдоподобия
ГЛАВА 5 Ошибки округления
Экономика страхования
1 Обзор и история вопроса
РАСЧЕТЫ И СТАТИСТИКА
Убытки от отзыва безаварийной пожарной безопасности
Модель расширения финансово-сбалансированной бонусно-малой системы
Bonus-malus: Come funziona | Assicurazione.Это
Подробная информация .. Когда использовать вычисляемые столбцы и вычисляемые поля
Перейти к основному содержанию
Microsoft Расчет производственных затрат в Excel
Расчет себестоимости товаров в торговле
Формулы для расчета плановой себестоимости продукции в Excel

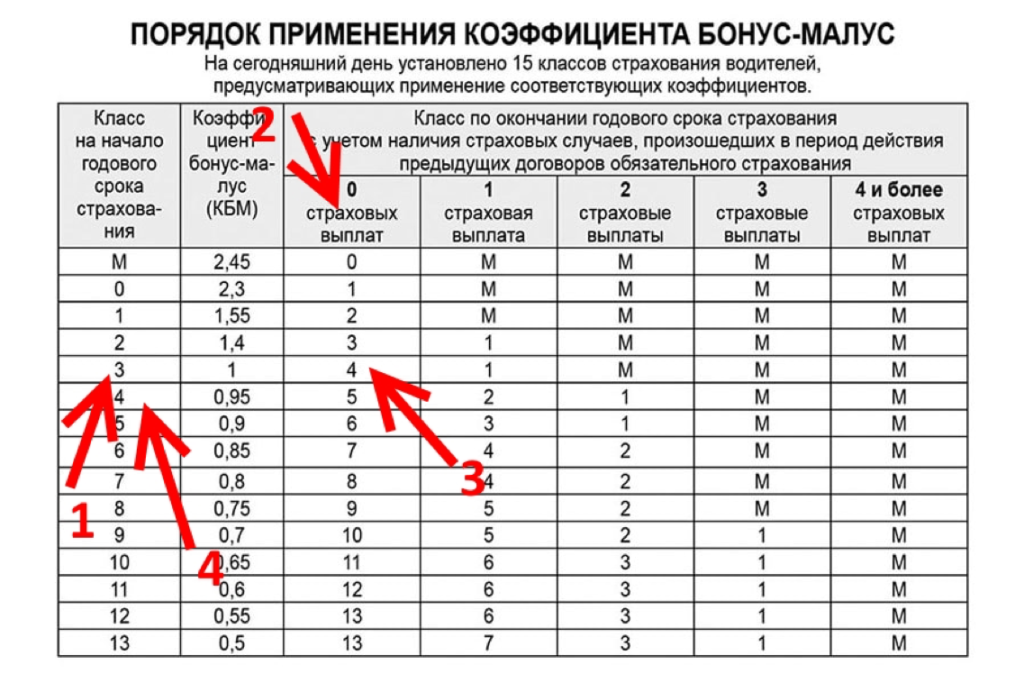 4
4
 В нашем примере это 1 класс аварийности.
В нашем примере это 1 класс аварийности. 45
45 55
55 55
55
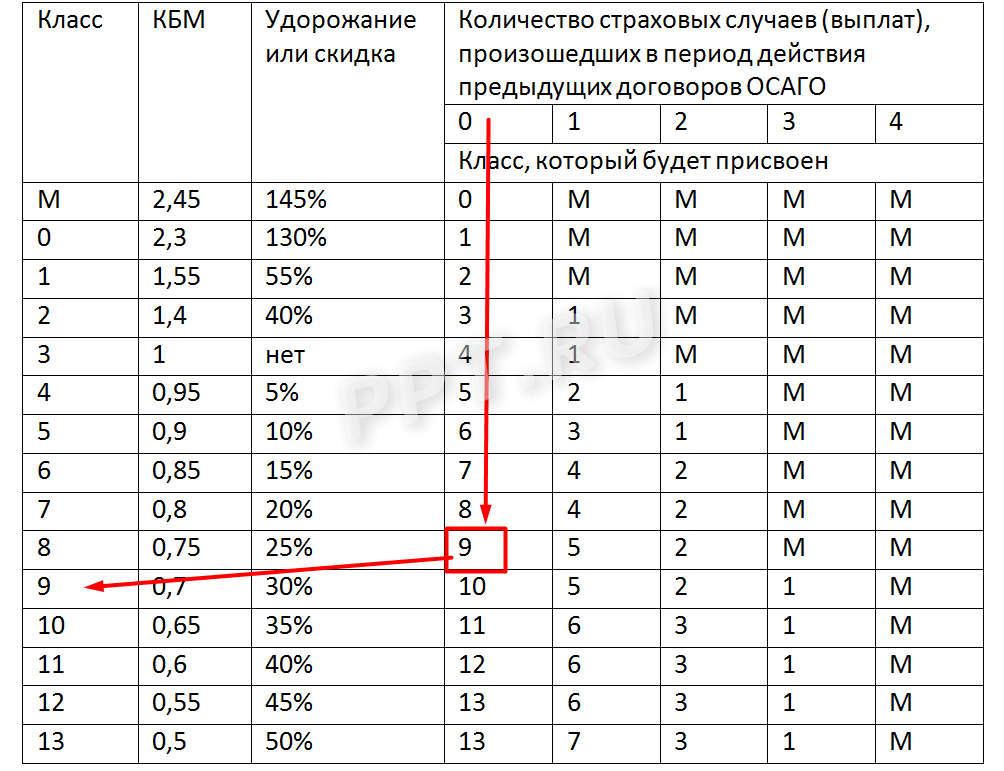 Проверьте класс водителя на сайте РСА. Информацию о классе уточняйте в страховом договоре. Некоторые компании прописывают такие сведения отдельно. А вот остальные источники считаются недостоверными.
Проверьте класс водителя на сайте РСА. Информацию о классе уточняйте в страховом договоре. Некоторые компании прописывают такие сведения отдельно. А вот остальные источники считаются недостоверными.